I have formulated a tentative possible solution. I leave for the mathematicians to judge.
As my math really sucks, what I did was what I tend to be better at, which is intuitive logic.
So here is a logical attempt at a solution to
Bertrand's paradox.
Please refer to the
Wikipedia article, I use their numbering of the methods of solution.
Fig. A
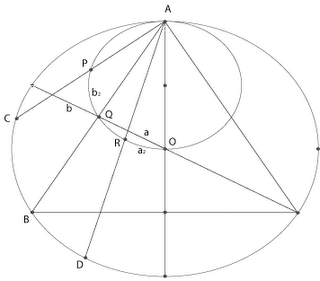
Fig. A shows method 1
- It is only necessary to consider the left half of the circle.
- The midpoints of the chords AC, AB and AD, which are P, Q and R, lie on the circumference of the inner smaller circle.
- The midpoints of possible chords which are longer than a side of the inscribed equilateral triangle lie on the arc QO, which is 1/3 of the left half of the circumference of the inner circle.
- The midpoints of possible chords which are shorter, lie on an arc AQ which is 2/3 of the left half of the inner circle.
It would seem obvious that the probability of the length of a chord randomly chosen, to be longer than a side of the triangle is 1/3. This solution however, is incompatible with methods 2 & 3.
Here is a possible reconciliation.
- The problem is determining the probability of the chord being longer.
- A chord has 2 properties. Length & Orientation.
- Therefore, there cannot possibly be chords without either or neither. i.e. chords that have orientation but no length, chords that have length but no orientation, or chords that have neither, cannot exist. viz. All chords have both Length and Orientation
- For a chord with x length, there are infinite possible orientations.
- For a chord with orientation y, there are infinite possible lengths from zero to the length of the diameter.
- Orientation can be held constant, i.e. for each length there is equal infinite possible orientations.
- We can do this by fixing orientation, i.e. consider only one orientation.
- This is in fact what is done in method 2.
- All the midpoints of chords considered in method 2 lies along the radius which is a straight line. Therefore all of their orientations are the same.
In Fig. A the the midpoints of chords with different length and orientation form the arc
a2 and
b2. Because the chord is projected onto the outer circle, and not a circle with a center point at A, this distorts the correspondence between length and orientation. While orientation changes constantly with each degree of angle, the lengths corresponding to each successive orientation does not. Each degree thus represents different proportions of possible lengths. The result being disproportionately more chords (shorter) are represented by the arc
b2, than by
a2 (longer). But orientation was held constant. This calculation results in a distorted false probability.
A correction can be applied to the resulting false probability of 1/3 to yield the correct (i think) probability of 1/2, which can be found by method 2.
Note: In the following calculation,
D is the diameter
Method 3 uses the relative distribution of midpoints in and outside of the inner circle to acquire a probability of 1/4.
Fig. B
Fig. B shows method 3.
- The areas of the 2 circles, can be represented by 2 rectangles of similar area .(see animation)
- The formula for the area of a circle is pi*r^2.
- The length of the rectangle is pi*r.
- The height of the rectangle is r.
- Therefore its area is equal to the larger circle.
- The reasoning is similar for the smaller circle.
- The height (r) can also be thought of as a dimension, which represents length of chord (by virtue of correspondence to a visualization of Archimedes' proof).
- The length (pi*r) can similarly represent orientation.
- Any point within the larger rectangle has coordinates representing length and orientation.
- The smaller circle, represented by the smaller rectangle, claims to contain midpoints of chords longer, and therefore all possible chords longer, than a side of the triangle.
- The smaller rectangle proves otherwise. The height of the smaller rectangle being half of the length of the larger rectangle represents correctly half of the possible lengths of the chord being longer than a side of the triangle. However the area of the smaller rectangle does not take into account all possible orientations of those chords. Namely only half. As the length of the smaller rectangle is half of the big one. This unfortunately results in a probability of 1/4, which is half of that of a correct solution.
click on image to view animation: visualization of Archimedes' proof (by Bettina Richmond) 
representation of areas of circles in method 3. (not drawn to scale)
But why does calculating the area of the smaller circle leave out half of the original orientations taken into account by the area of the larger circle?
The next diagram makes it obvious.
The arc ABC is twice as long as the corresponding arc of the smaller circle, DEF. However, the orientations they represent are supposed to be the same. The angle SOR and TOU are the same. But the arc SR and TU are different in length. The same goes for the areas a and b.
The arcs ABC and DEF are respectively represented as pi*r and 1/2 pi*r in the rectangles above. We cannot work directly with infinity of course. We don't can't enumerate the magnitude of infinity. We can't count the infinite possible orientations. What we can do however, is keeping it constant as we work with another variable. In this case the length of chord. Methods 1 & 3 have been shown not to have kept orientation constant, while method 2 has. That is why method 2 gives a correct answer.
However, we can also show how off the mark our calculations were. pi*r represents the infinite possible orientations. 1/2 pi*r represents
half of that infinity. That is why the probability obtained using method 3 (1/4) is
half of what is correct (1/2).
That's it! The probability of the length of a randomly drawn chord in the circle being longer than a side of the inscribed equilateral triangle is not all 1/3, 1/2 and 1/4.
It is 1/2.
And I believe I have proven it, if not mathematically, then logically.
Please do criticize me, as I have said, my math sucks! I might have made a terrible mistake here.
Labels: mathematics
see that in the box?
Fig. A shows method 1
Fig. B shows method 3.
The arc ABC is twice as long as the corresponding arc of the smaller circle, DEF. However, the orientations they represent are supposed to be the same. The angle SOR and TOU are the same. But the arc SR and TU are different in length. The same goes for the areas a and b.